Problemas resueltos de choques (II)

Dos esferas iguales de masas 6 kg y 20 cm de radio están montadas como se indica en la figura, y pueden deslizar a lo largo de una varilla delgada de 3 kg de masa y 2 m de longitud. El conjunto gira libremente con una velocidad angular de 120 rpm respecto a un eje vertical que pasa por el centro del sistema. Inicialmente los centros de las esferas se encuentran fijos a 0.5 m del eje de giro. Se sueltan las esferas y las esferas deslizan por la barra hasta que salen por los extremos. Calcular:

a) la velocidad angular de rotación cuando los centros de las esferas se encuentran en los extremos de la varilla. Qué principio físico aplicas?. Por qué?.

b) Hallar la energía cinética del sistema en los dos casos.

Dato momento de inercia de una esfera y de la varilla

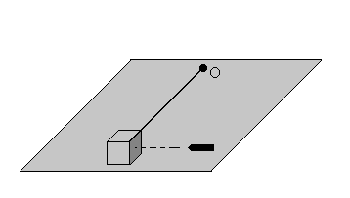Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una superficie horizontal sin fricción, está sujeto a una barra rígida de longitud 2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el otro al centro del cubo. Una bala de masa 50 g y velocidad 200m/s se incrusta en el cubo a la altura de su centro de masa (en la dirección perpendicular al cubo, tal como se muestra en la figura)

. ¿Cuál es la velocidad angular del sistema después del choque?. ¿Qué principio físico has aplicado?. ¿por qué? ¿Se conserva la energía en esta colisión?.

Momentos de inercia respecto de un eje que pasa por el cm del cubo: y de la varilla

Un péndulo está formado por una varilla de 200 gr de masa y 40 cm de longitud y dos esferas macizas: la superior de 500 gr y 5cm de radio y la inferior de 400 gr y 4 cm de radio, equidistantes 8 cm de los extremos de la barra. El péndulo se haya suspendido de un eje perpendicular a la varilla que pasa por el centro de la esfera superior. Sobre el centro de la esfera inferior incide una bala de 50 gr y 10 m/s de velocidad que queda alojada en el centro de la esfera.

¿Pasará por la posición vertical de equilibrio inestable?. En caso afirmativo, ¿con qué velocidad angular?.

Datos: Momento de inercia: de una varilla ml²/12, y de una esfera 2mr²/5

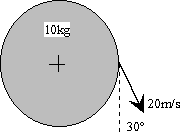Un disco de masa 10 kg y radio 0.5 m está en reposo y puede girar en torno a un eje perpendicular al disco y que pasa por su centro. En la periferia del disco hay un dispositivo de masa despreciable, que permite lanzar un objeto de 200 g a una velocidad de 20 m/s, en la dirección y sentido indicado en la figura.

¿Qué principio físico aplicas?. Razona la respuesta

Calcular:

La velocidad angular del disco después del disparo
El sentido en que gira.
La variación de energía

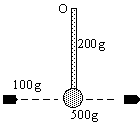Una bala de 100 g que lleva una velocidad horizontal de 50 m/s choca con el centro del cilindro de un péndulo. Después del choque la bala se mueve con una velocidad de 40 m/s. El péndulo gira alrededor de O y está formado por una varilla delgada de 200 g de masa y 20 cm de longitud, y un cilindro de 500 g de masa y 5 cm de radio.

Calcular el ángulo máximo que gira el péndulo como consecuencia del choque y la energía perdida en el mismo.

Momentos de inercia: Ivarilla=ML²/12 respecto a un eje que pase por su c.m. pependicular a la varilla, Icilindro=MR²/2 respecto a un eje perpendicular a la base que pase por su c.m.

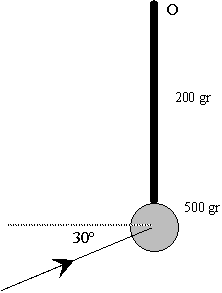Una bala de 100 gr que lleva una velocidad de 12.5 m/s choca con el centro del disco de un péndulo, tal como se muestra en la figura. Después del choque, la bala queda empotrada en el centro del disco. El péndulo que gira en torno a un eje perpendicular que pasa por O, está formado por una varilla delgada de 200 gr de masa y 20 cm de longitud y una lenteja de 500 gr de masa y 5 cm de radio.

Calcular la velocidad angular del sistema inmediatamente después del choque. ¿Qué principio físico aplicas?, ¿por qué?.
Calcular el ángulo máximo que gira el péndulo como consecuencia del choque, y la energía perdida en el mismo.

El momento de inercia de la varilla es ML²/12, y del disco MR²/2, respecto a un eje perpendicular que pasa por su c.m. respectivo. (Tómese g=9.8 m/s²)

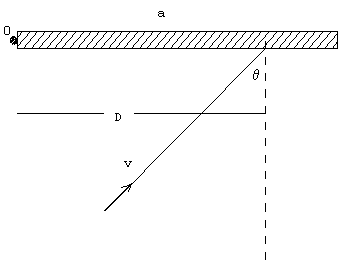Obtener la fórmula del momento de inercia de una puerta de masa M, altura b y anchura a, respecto a un eje que pase a lo largo de su lado b, tal como se indica en la figura.

Una puerta de masa M, se encuentra en reposo y es golpeada por una bola de masilla de masa m, tal como se muestra en la figura. La velocidad de la bola de masilla es v, y su dirección inicial es horizontal, formando un ángulo q con la normal a la cara de la puerta, impactando a una distancia D del eje de la misma. Después de la colisión la bola se queda pegada a la puerta. Obtener:

La expresión de la velocidad de la puerta después de la colisión.
La variación de energía cinética del sistema (puerta más bola de masilla).

Datos m = 1.1 kg, M = 35 kg, a = 73 cm, b = 190 cm, D = 62 cm, q = 22º, v = 27 m/s.