Problemas resueltos de choques (I)

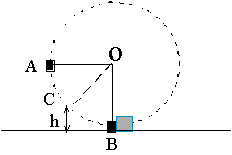
El péndulo simple de la figura consta de una masa puntual m1=20 kg, atada a una cuerda sin masa de longitud 1.5 m. Se deja caer desde la posición A. Al llegar al punto más bajo de su trayectoria, punto B, se produce un choque perfectamente elástico con otra masa m2=25 kg, que se encuentra en reposo en esa posición sobre una superficie horizontal sin rozamiento. Como consecuencia del choque, la masa m1 rebota hasta alcanzar la posición C a altura h del suelo. Determinar

1. La velocidad de m₁ al llegar a la posición B antes del choque y la tensión de la cuerda en ese instante.
2. Las velocidades de m₁ y m₂ después del choque.
3. La energía cinética que pierde m₁ en el choque.
4. La altura h al que asciende la masa m₁ después del choque.

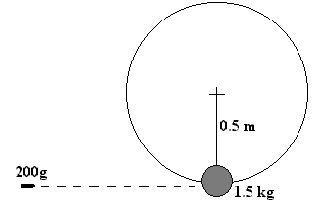Una bala de 200 g choca con un bloque de 1.5 kg que cuelga de una cuerda, sin peso de 0.5 m de longitud, empotrándose en el bloque. A este dispositivo se le denomina péndulo balístico. Responder a las siguientes cuestiones:

• ¿Cuál debe ser la velocidad de la bala para que el péndulo se desvíe 30º?
• Determinar la tensión de la cuerda en el punto más alto de la trayectoria circular, cuando la velocidad de la bala es de 45 m/s.
• ¿Describirá el bloque un movimiento circular cuando la velocidad de la bala es de 40 m/s?. Razónese la respuesta. En caso negativo, determinar su desplazamiento angular.

Una bala de 50 g de masa se empotra en un bloque de madera de 1.2 kg de masa que está suspendido de una cuerda de 2 m de larga. Se observa que el centro de masa del bloque y la bala se eleva 40 cm. Encontrar el módulo de la velocidad de la bala. La tensión de la cuerda cuando el ángulo que forma con la vertical es de 10º.

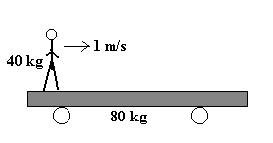Desde el extremo de una plataforma móvil de 80 kg, inicialmente en reposo, un niño de 40 kg corre hacia el otro extremo a una velocidad constante de 1 m/s. Determinar la velocidad de la plataforma y el sentido de su movimiento. ¿Qué principio físico aplicas?

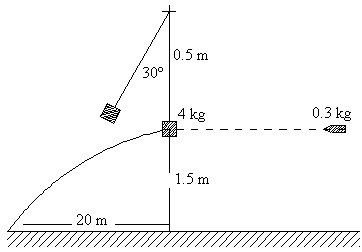Una bala de masa 0.3 kg y velocidad desconocida choca contra un saco de 4 kg suspendido de una cuerda de 0.5 m de larga y en reposo. Después del choque el saco se eleva hasta que la cuerda hace un ángulo de 30º con la vertical, mientras tanto la bala describe una parábola, estando el punto de impacto a 20 m de distancia horizontal y 1.5 m por debajo. Calcular: La velocidad del saco y la de la bala inmediatamente después del choque La velocidad de la bala antes del choque y la energía perdida en el mismo La tensión de la cuerda cuando esta hace 10º con la vertical

Una partícula de 5 kg de masa moviéndose a 2 m/s choca contra otra partícula de 8 kg de masa inicialmente en reposo.Si la primera partícula se desvió 50º de la dirección original del movimiento. Hallar la velocidad de cada partícula después del choque.  Se supone que el choque es elástico

Desde un punto B situado a 7.65 m del suelo se deja caer una esfera de madera de 460 gr de peso; en el mismo instante, desde otro punto A situado a igual nivel que B y distante de éste 270 m se dispara un proyectil de cobre de 20 gr, el cual alcanza la esfera centralmente durante su caída, quedando empotrada en la misma y alcanzando ambos el suelo a 7.5 m del pie de la vertical que pasa por B. Determinar el ángulo de tiro q para que se produzca el choque en el punto C. Calcular la velocidad de disparo de la bala v0 (se consideran los cuerpos como masas puntuales y no se tendrá en cuenta la resistencia del aire).

Una bala de 10 g se incrusta en un bloque de 990 g que descansa sobre una superficie horizontal sin fricción, sujeto a un resorte, tal como se ve en la figura. El impacto comprime el resorte 15 cm. Del resorte se sabemos que una fuerza de 2 N produce una comprensión de 0.25 cm. Calcular La constante elástica del muelle La velocidad del conjunto bloque + bala justo después del choque La velocidad de la bala antes del choque.

Una partícula de masa 4 kg y velocidad 2 m/s choca contra otra de 3 kg que está en reposo. La primera se desvía –45º respecto de la dirección inicial y la segunda 30º.

• Calcular las velocidades de ambas partículas después del choque.
• ¿Es elástico?

Tres partículas A, B y C de masas mA = mB = m y mC = 2m, respectivamente se están moviendo con velocidades cuyo sentido se indica en la figura y de valor vA = vB = v y vC = 2v. Se dirigen hacia el origen del sistema de coordenadas al que llegan en el mismo instante. Al colisionar A y B quedan adheridas y salen en la dirección indicada con velocidad v/2. ¿Qué principio aplicas para resolver el problema?. ¿Por qué?. Determinar: la velocidad y dirección sale la partícula C. ¿Es un choque elástico?. Razona la respuesta.

Un resorte vertical de constante K=1000 N/m sostiene un plato de 2 kg de masa. Desde 5m de altura respecto al plato se deja caer un cuerpo de 4 kg que se adhiere a él. Calcular la máxima compresión del resorte