![]() Di si las afirmaciones siguientes son verdaderas o
falsas, y por qué.
Di si las afirmaciones siguientes son verdaderas o
falsas, y por qué.
a• Todos los puntos de un cuerpo que gira tienen la misma velocidad angular.
b • Todos los puntos de un cuerpo que gira tienen la misma velocidad lineal.
c • El momento de inercia depende de la situación del eje de rotación.
d • Si el momento neto de las fuerzas que actúan sobre un sólido es cero, el momento angular es cero.
e • Si el momento neto de las fuerzas que actúan sobre un sólido es cero, la velocidad angular no cambia.
f • Si la fuerza neta aplicada sobre un cuerpo es cero este cuerpo tiene momento angular cero.
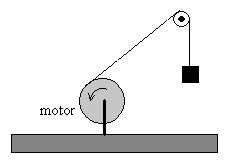 |
Un bloque de 2000 kg está suspendido en el aire por un cable de acero que pasa por una polea y acaba en un torno motorizado. El bloque asciende con velocidad constante de 8 cm/s. El radio del tambor del torno es de 30 cm y la masa de la polea es despreciable. |
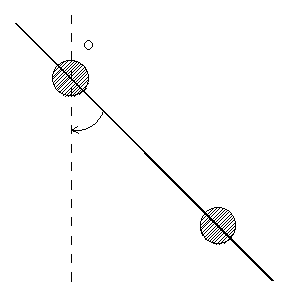 |
Un péndulo compuesto está formado por una varilla de 200 g de masa y 40
cm de longitud y dos esferas macizas de 500 g y 5 cm de radio, equidistantes 8 cm de los
extremos de la barra. El péndulo se haya suspendido de un eje perpendicular a la varilla
que pasa por el centro de una de las esferas, y es desviado 65º de la posición de
equilibrio estable. Determinar la velocidad angular del péndulo cuando, una vez soltado, retorna a la posición de equilibrio estable |
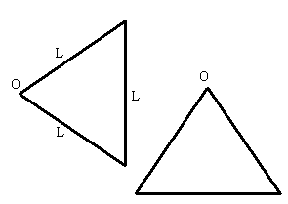 |
Un sólido está formado por tres barras iguales de longitud L=2 m y de
masa M=20 kg en forma de triángulo equilátero, tal como se muestra en la figura.
Momento de inercia de la varilla Ic=ML2/12 |
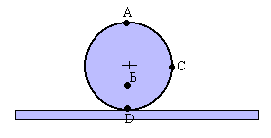 |
Hallar y dibujar el vector velocidad de los puntos del disco que se indican en la figura. El disco rueda sin deslizar, tiene un radio de 5 cm, y se mueve (su c.m.) con velocidad de 3m/s. A (arriba), C (a la derecha) y D (abajo) están en la periferia, y B 2.5 cm por debajo del centro del disco |
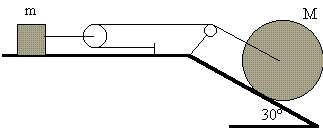 |
Un bloque de masa m=20 kg, unido mediante una cuerda a una polea sin masa desliza a lo largo de una mesa horizontal con coeficiente de rozamiento dinámico m=0.1. La polea está conectada mediante otra cuerda al centro de un carrete cilíndrico de masa M=5 kg, y radio R=0.1 m que rueda sin deslizar a lo largo de un plano inclinado 30º (véase la figura). |
a) Relacionar la aceleración del bloque y del centro de masas del cilindro.
b) Calcular la aceleración del centro de masas del cilindro y las tensiones de las cuerdas.
c) Calcular la velocidad del centro de masas del cilindro cuando ha descendido 3 m a lo largo del plano inclinado, partiendo del reposo (hacer esta última pregunta empleando el balance energético).
Dato: Icilindro = 1/2 MR2
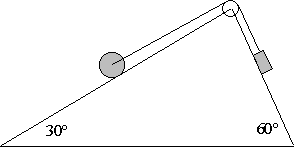 |
Un bloque y un cilindro de 2 y 8 Kg respectivamente, están unidos por
un hilo inextensible y sin peso que pasa por una polea en forma de disco de 0.5 Kg de masa
y 20 cm de radio, situada en la unión de dos planos inclinados de 30º y 60º de
inclinación. Sabiendo que el coeficiente de rozamiento entre el bloque y el plano es de
|
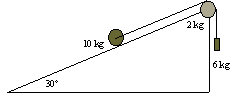 |
Un bloque de 6 kg y una esfera de 10 kg están unidos por un hilo
inextensible y sin peso que pasa a través de una polea en forma de disco de 2 kg de masa.
La esfera rueda sin deslizar a lo largo de un plano inclinado 30º. Hallar |
·
La(s) tensión(es) de la cuerda.· La aceleración del sistema
La velocidad de la esfera y del bloque cuando se han desplazado 1.5 m partiendo del reposo (emplear dos procedimientos para el cálculo de este apartado). Dato, el momento de inercia de la esfera es 2/5 mr2.
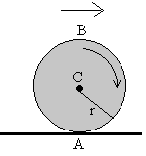 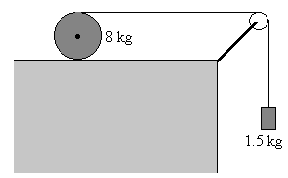 |
En lafFigura de la izquierda, un disco de radio r rueda sin
deslizar a lo largo de un plano horizontal. Sabiendo que la aceleración del centro de
masas es ac y la aceleración angular de rotación alrededor del c.m. es
a . Determinar la aceleración del punto B (punto más alto del
disco)?. Utilizando el resultado anterior, en el sistema de la figurade la derecha, calcular la aceleración del c.m. del disco, la aceleración del bloque, la tensión de la cuerda y la fuerza de rozamiento en el punto A. El disco tiene un radio de 30 cm y rueda sin deslizar a lo largo del plano horizontal. La polea tiene una masa despreciable. |
Calcúlese la velocidad del bloque una vez que haya descendido 2 m partiendo del reposo. (aplicar el balance energético en este apartado). ¿Hay que incluir en el balance energético el trabajo de la fuerza de rozamiento en el movimiento de rodar sin deslizar?
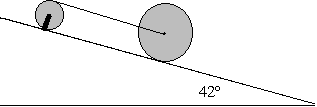 |
En la figura se muestra un cilindro de 4.5 kg de masa que rueda sin deslizar, a lo largo de un plano inclinado 42º con la horizontal. El centro del cilindro está unido mediante una cuerda al borde de una polea en forma de disco de 2.2 kg de masa y 85 mm de radio. Sabiendo que en el eje de la polea existe un rozamiento cuyo momento es de 1.3 Nm. Calcular: |
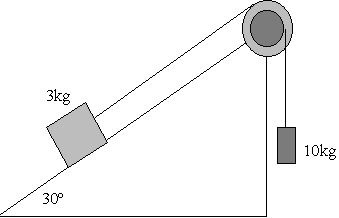 |
Sobre un plano inclinado 30º y que ofrece una resistencia al
deslizamiento de coeficiente m=0.2, desliza un bloque de 3 kg
de masa unido a una cuerda que se enrolla en la periferia de una polea formada por dos
discos acoplados de 1 kg y 0.5 kg y de radios 0.3 m y 0.1 m respectivamente. De la cuerda
enrollada al disco pequeño pende un bloque de 10 kg de peso. Calcular:
La velocidad de cada cuerpo si el bloque de 10 kg desciende 2 m partiendo del reposo (emplear dos procedimientos distintos para este apartado). |
 |
Un disco de 2 kg. de masa y radio 30 cm rueda sin deslizar a lo largo de
un plano horizontal, una cuerda arrollada a una hendidura hecha en el disco, de radio 15
cm está unida a través de una polea en forma de disco de masa 0.5 kg a un bloque de 10
kg, que pende del extremo de la misma tal como se indica en la figura. Calcular:
|
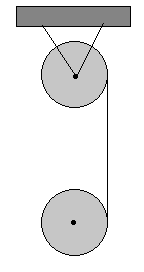 |
Dos discos iguales de masa m y radio R, están
dispuestos como se indica en la figura. Calcular
|