 |
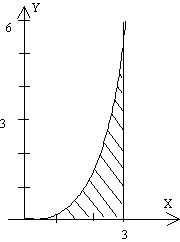
Determinar la posición del centro de masa de la siguiente figura plana y homogénea, formada por la región comprendida entre la parábola y=2x2/3 y el eje X, y la recta x=3 |
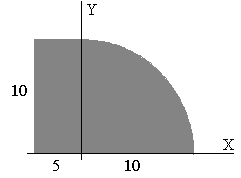 |
Determinar la posición del centro de masa de la siguiente figura plana y homogénea formada por un rectángulo y un cuarto de círculo |
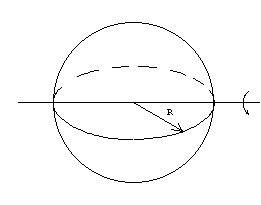 |
Calcular el momento de inercia de una esfera de masa M y radio R. |
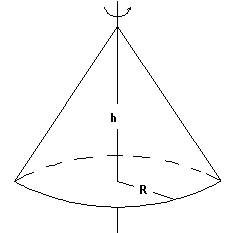 |
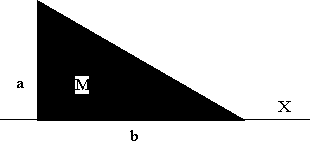
Calcular el momento de inercia de un cono macizo de masa M, altura h, y radio de la base R, respecto de su eje. |
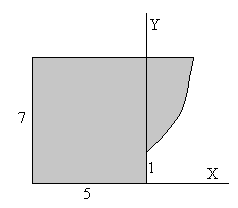 |
Determinar la posición del centro de masa de la pieza plana homogénea de la figura. La parte curva corrsponde a la porción de parábola y=3x2/2+1. |
 |
|