Problemas resueltos de oscilaciones

Una partícula oscila con un movimiento armónico simple de tal forma que su desplazamiento varía de acuerdo con la expresión x=5 cos(2t+p /6) . Donde x está en cm y t en s. En t=0 encuentre

• el desplazamiento,
• su velocidad,
• su aceleración.
• Determinar el periodo y la amplitud del movimiento

Componer los siguientes MAS: x₁=2sen(wt+5p/4) e x₂=5sen(wt+5p/3)

Una partícula de 300 g de masa está unida a un muelle elástico de constante k=43.2 N/m y describe un movimiento armónico simple de 20 cm de amplitud. Sabiendo que en el instante t=0 se encuentra a 10 cm del origen moviéndose hacia la izquierda, determinar:

• Las ecuaciones de la posición, velocidad y aceleración en función del tiempo.

• Las energías potencial, cinética y total en el instante inicial y en cualquier instante.

• Valores de t en los que la partícula pasa por el origen.

Un cuerpo está unido a un muelle horizontal de constante k=5N/m. El muelle se alarga 10 cm y se suelta en el instante inicial t=0. Hallar:

• la frecuencia, el período y la amplitud del movimiento. Escribir la ecuación del M.A.S.
• ¿cuál es la velocidad máxima? ¿Cuál es la aceleración máxima?
• ¿En qué instante pasa el cuerpo por primera vez por la posición de equilibrio?

Un resorte horizontal tienen una constante recuperadora de 48 N/m. En el extremo del resorte se coloca una masa de 0.75 kg y se estira el resorte 0.2 m a partir de la posición de equilibrio, soltándose a continuación, momento en el que se empieza a contar el tiempo. Hallar:

• El periodo de la oscilación.
• La ecuación del M.A.S.
• El (los) instante(s) en el(los) que el móvil pasa por la posición x=-0.1 m, después de haber pasado por el origen.
• Los valores de la velocidad, aceleración, energía cinética, potencial y total del móvil en dicho(s) instante(s).

El péndulo de un reloj tiene un periodo de 2 s cuando g=9.8 m/s². Si la longitud del péndulo, L, se incrementa en un milímetro y sabiendo que el período para pequeñas oscilaciones viene dado por ¿cuánto se atrasará el reloj en 24 horas?

Hallar el periodo de la oscilación de un bloque de masa M=250 g unido a los dos muelles elásticos de la figura. Se supone que no hay rozamiento.

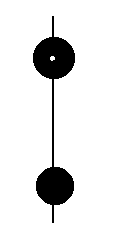Un péndulo está formado por una varilla de 200 gr de masa y 40 cm de longitud y dos esferas macizas: la superior de 500 gr y 5cm de radio y la inferior de 400 gr y 4 cm de radio, equidistantes 8 cm de los extremos de la barra. El péndulo se haya suspendido de un eje perpendicular a la varilla que pasa por el centro de la esfera superior. Hállese el periodo. Si ahora se separa el péndulo 10º de la posición de equilibrio y se suelta, empezándose en ese momento a contar el tiempo. Escríbase la ecuación del M.A.S. Datos: Momento de inercia: de una varilla ml2/12, y de una esfera 2mr2/5