Dinámica de la partícula (II)

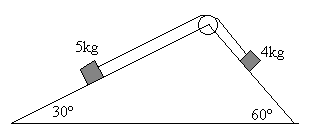
Dos bloques de 5 y 4 Kg están unidos por una cuerda que pasa por una polea de masa despreciable, ambos deslizan sobre planos inclinados de 30º y 60º, respectivamente. Sabiendo que el coeficiente din mico de rozamiento en ambos planos vale 0.1. Calcular: la aceleración del sistema, la tensión de la cuerda, la velocidad que adquieren los bloques cuando se desplazan 3 m a lo largo de los planos inclinados respectivos, partiendo del reposo. (Emplear dos procedimientos de cálculo para este apartado, comprobando que se obtienen los mismos resultados).

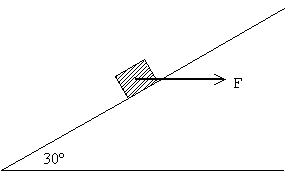Un bloque de 4 kg asciende a lo largo de un plano inclinado 30º, al serle aplicada una fuerza F horizontal, tal como se indica en la figura. Sabiendo que el bloque, parte del reposo, en la base del plano inclinado, y alcanza una velocidad de 6 m/s después de recorrer 10 m a lo largo del plano. Determinar el valor de la fuerza F. En dicha posición x=10 m se deja de aplicar la fuerza F, determinar el desplazamiento total del móvil a lo largo del plano hasta que se para. El coeficiente de rozamiento entre el cuerpo y el plano inclinado es 0.2

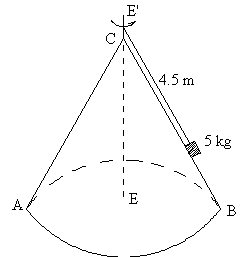Un cuerpo de 5 kg de masa se encuentra sobre una superficie cónica lisa ABC, y está girando alrededor del eje EE' con una velocidad angular de 10 r.p.m. Calcular: La reacción de la superficie cónica La tensión de la cuerda La velocidad angular a la que ha de girar el cuerpo para anular la reacción de la superficie cónica.

La fuerza aplicada a un móvil de 2 kg de masa varía con el desplazamiento de acuerdo a la expresión F=-x²+4x-3 N. Si la velocidad del móvil en la posición x=0 es de 3 m/s, calcular la velocidad del móvil en la posición x=3 m.

La fuerza aplicada a un móvil de 2 kg de masa varía con el tiempo de acuerdo a la expresión F=t²+4t-3 N. Si la velocidad del móvil en el instante t=0 es de 3 m/s, calcular la velocidad del móvil en el instante t=3 s.

Un péndulo simple está formado por un hilo inextensible y de masa despreciable de 0.5 m de longitud del que cuelga una masa puntual de 2 kg. Si se separa de la posición de equilibrio y se suelta, calcular la tensión del hilo cuando el péndulo pasa de nuevo por la posición vertical. Tomar g=9.8 m/s².

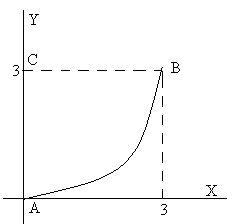Sobre una partícula actúa una fuerza F=2x2i+3y2j N. Hallar el trabajo realizado por dicha fuerza a lo largo del camino cerrado ABCA de la figura. El camino AB es una porción de la parábola y=x2/3.

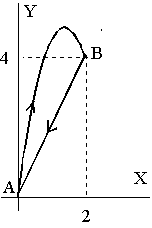Hallar el trabajo de la fuerza N a lo largo del camino ABA. El camino AB es el tramo de parábola .El camino BA es la recta que une el punto B de coordenadas (2,4) con el origen. ¿De qué tipo de fuerza se podría tratar?. Defínela

Una partícula de 2 kg se mueve en el plano XY bajo la acción de una fuerza cuyas componentes son F_x=-6p sen(p t/2), F_y=4p cos(p t/2), si en el instante inicial t=3 s, la partícula se encontraba en el punto (-12p , 0) y tenía una velocidad v₀=-4j m/s. Calcular:

• El vector posición y el vector velocidad en función del tiempo
• El momento de la fuerza F respecto del origen.
• El momento angular L de la partícula respecto del origen
• Comprobar que en el instante t,

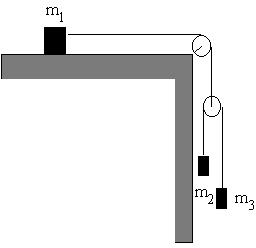Calcular la aceleración de los cuerpos m1, m2 y m3 de la figura.

Deducir la ecuación que nos da el valor mínimo del radio que puede tener una curva con peralte q para que un automóvil que la recorre con velocidad v m/s no deslice hacia el exterior, suponiendo que el coeficiente de rozamiento es m. Datos: v=144 Km/h, m=0.75, q=15º.

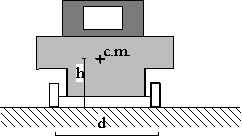
Suponer ahora, que la curva no tiene peralte, como se muestra en la figura, deducir la fórmula que nos dé el valor del radio mínimo para que el coche que va con velocidad v no vuelque, sabiendo que el centro de gravedad está a h metros del suelo y que la distancia entre ruedas es d metros. Con los datos v=144 Km/h, m=0.75, d=1.8 m y h=0.40 m. el coche volcará o deslizará hacia el exterior,

¿Cuál de las dos cosas hará antes?. Razónese la respuesta. (Resuélvase este apartado desde el punto de vista del observador NO inercial)