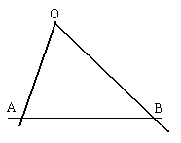Dinámica de la partícula (I)

Desde un mismo punto O se dejan caer a la vez dos cuerpos por dos planos inclinados OA y OB de diferentes pendientes y sin rozamiento. Estudiamos el paso de cada uno de los cuerpos por los puntos A y B situados sobre la misma horizontal. Comparar, justificando la respuesta Las aceleraciones de los dos cuerpos La velocidades de los dos cuerpos Los tiempos empleados en llegar a A y B.

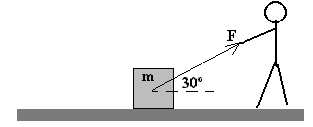La fuerza de rozamiento que actúa sobre el bloque vale m kmg en una de las siguientes situaciones (m k es el coeficiente dinámico de rozamiento). Razónese la respuesta

1. Cuando se ejerce una fuerza F, y el bloque se desplaza con velocidad constante
2. Cuando se ejerce una fuerza F, y el bloque está en reposo
3. Cuando se ejerce una fuerza F, y el bloque se mueve con aceleración
4. Cuando no actúa la fuerza F, y el bloque está en movimiento
5. Cuando no actúa la fuerza F, y el bloque está en reposo
6. Cuando se ejerce una fuerza F, y el bloque está a punto de empezar a moverse

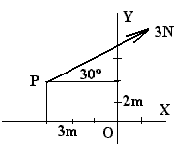Calcular el momento de la fuerza (módulo, dirección y sentido) de la figura respecto de O.

Sobre una cinta transportadora cae trigo a razón de 600 kg/min desde una tolva en reposo. La cinta se mueve con velocidad de 0.5 m/s.

• Calcular la fuerza F sobre la cinta que hace que la velocidad del sistema permanezca constante. Razonar la respuesta.

En el movimiento de un péndulo simple actúan tres fuerzas sobre la masa suspendida (la cuerda se considera sin masa): fuerza de la gravedad (peso), tensión de la cuerda y resistencia del aire.

• Dibujar las fuerzas y la trayectoria del péndulo.
• ¿Todas las fuerzas realizan trabajo?
• ¿Cuál de ellas realiza un trabajo negativo durante todo el tiempo que dura el movimiento?
• Escribir el principio del trabajo y la energía para el péndulo para cualquier posición.

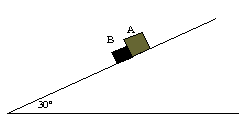Sobre un tablero inclinado un ángulo de 30º se colocan dos cuerpos A y B de masa 4 y 3 kg respectivamente. Los coeficientes de rozamiento entre el bloque A y el plano inclinado es 0.1, y entre el bloque B y dicho plano 0.2.

• ¿Cómo deslizarán los cuerpos, juntos o separados?.
• Hállese la aceleración de cada cuerpo y la reacción en la superficie de contacto (si la hubiere).
• Hallar la velocidad común o de de cada cuerpo después de haberse desplazado 5 m a lo largo del plano inclinado, partiendo del reposo. (Emplear en este apartado dos procedimientos de cálculo: cinemática y balance energético)

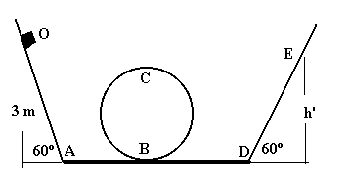El esquema de la figura representa dos planos inclinados 60º sin rozamiento, dos planos horizontales AB =BD= 1m con rozamiento al deslizamiento de coeficiente m =0.1 y una circunferencia vertical sin rozamiento de radio R=1 m. Una partícula de masa m=300 g se abandona sin velocidad inicial y recorre el camino OABCDE. Se pide Si la altura de O es de 3 m calcular la velocidad de la partícula en A, B, C y D ¿Cuál será la reacción en los puntos B y C? ¿Cuánto ascenderá por el plano inclinado DE?.

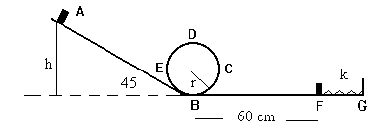Un bloque de 600 g se suelta en la posición A, desliza a lo largo del plano inclinado de 45º de inclinación hasta B, a continuación describe el bucle BCDEB, desliza a lo largo del plano horizontal BF y finalmente comprime un muelle de constante k=500 N/m cuyo extremo libre dista 60 cm de B.

• Calcular la máxima deformación del muelle, sabiendo que la altura h de A es de 2.5 m, el radio del bucle r=0.5 m, y el coeficiente dinámico de rozamiento en el plano horizontal BG e inclinado AB es de 0.3. Se supone que no hay rozamiento en el bucle.
• Hallar la reacción en la posición D. (Tomar g=9.8 m/s²)

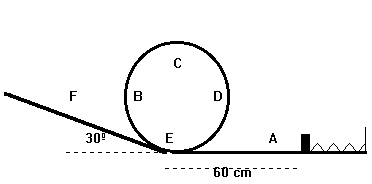Un bloque de 600 gr se suelta cuando un muelle, de constante 500 N/m está comprimido 150 mm. Luego se traslada a lo largo del bucle de 50 cm de diámetro siguiendo la trayectoria ABCDEF. Sabiendo que la distancia entre el bloque y la base del bucle en el momento en que se suelta el bloque es de 60 cm, que solamente existe rozamiento en las superficies planas , cuyo coeficiente dinámico vale 0.3. Calcular:

· La reacción en las posiciones A, C, E y F.

· La distancia que recorrerá la partícula a lo largo del plano inclinado hasta pararse, una vez que haya salido del bucle.

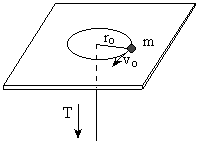Se sujeta una masa m a una cuerda que pasa por un pequeño orificio en una mesa sin fricción (ver figura). En un principio la masa se encuentra moviéndose en un círculo de radio ro=0.3m con velocidad vo=1.5m/s. En este instante se tira lentamente de la cuerda por la parte de abajo disminuyendo el radio del círculo hasta r=0.1m.

• ¿Cuál es la velocidad de la masa para ese valor del radio?

• ¿Cuánto vale la tensión para ese valor del radio?

• Encontrar la expresión de la tensión para cualquier valor de r.

• ¿Cuánto trabajo se realiza al mover m de ro a r?

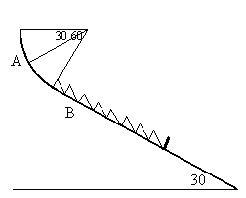Una pista de patinaje tiene la forma indicada en la figura. El primer tramo lo constituye un arco de 60º de una circunferencia de 30 m de radio. El segundo tramo discurre por un plano inclinado tangente a la circunferencia en el punto inferior del arco. En el tramo plano se coloca un muelle (parachoques) de constante k=40 N/m cuyo extremo libre coincide exactamente con el final del tramo circular. Un patinador de 70 kg de masa se deja deslizar con velocidad inicial nula desde el extremo superior del primer tramo circular siendo detenido finalmente por la acción del resorte. A lo largo de la pista no hay rozamiento. Determinar:

• La reacción de la pista en A y B. El punto A hace un ángulo de 30º con la horizontal, y B es un punto del plano inclinado.
• La distancia que habrá comprimido el muelle cuando el patinador se detiene por completo.

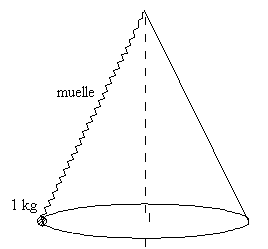Enganchamos una partícula de 1 kg a un resorte de masa despreciable cuya longitud natural es de 48 cm y la constante recuperadora 10 N/cm. Lo hacemos girar como un péndulo cónico con una velocidad angular constante de 60 r.p.m. Calcular: El alargamiento del resorte. El ángulo que forma la altura del cono con la generatriz.

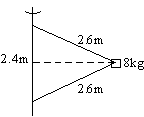Un bloque de 8 kg está sujeto a una barra vertical mediante dos cuerdas. Cuando el sistema gira alrededor del eje de la barra las cuerdas están tensadas, tal como muestra la figura. ¿Cuántas revoluciones por minuto tiene que dar el sistema para que la tensión de la cuerda superior sea de 150 N? ¿Cuál es entonces la tensión de la cuerda inferior?

Un vagón de ferrocarril está abierto por arriba y tiene un área de 10 m², se mueve sin fricción a lo largo de rieles rectilíneos con velocidad de 5 m/s, en un momento dado comienza a llover verticalmente a razón de 0.001 litros/(cm²s). La masa inicial es de 20000 kg. Calcular, razonando las respuestas:

• La velocidad del vagón en función del tiempo
• La aceleración
• La fuerza necesaria para mantenerlo a velocidad constante de 5m/s.