OBJETO DE LA EXPERIENCIA	ANALISIS DE DATOS
METODOLOGIA	PROGRAMA DE SIMULACION "AMBOE"
FUNDAMENTOS TEORICOS	CUESTIONARIO
MATERIALES A UTILIZAR	BIBLIOGRAFIA
TECNICA OPERATORIA	HOJA DE DATOS
	Abrir archivo WORD

OBJETO DE LA EXPERIENCIA

 

Examinar el formalismo matemático que describe al campo eléctrico resolviendo la ecuación de Laplace y graficando el potencial en los puntos interiores a una región limitada por dos electrodos empleando utilitarios matemáticos de PC.

    METODOLOGIA

 

Establecer y mapear un campo eléctrico en la región comprendida entre dos electrodos de geometría sencilla. Mediante una planilla de  cálculo electrónica, aplicar el método de diferencias finitas para resolver la ecuación de Laplace que describe la situación particular de la experiencia. Comparar los resultados teóricos con los experimentales.

 Fundamentos teóricos

    Haremos la deducción del método de diferencias finitas para el  problema bidimensional. Así, consideremos una función V(x,y), la cuál  desarrollamos alrededor de un punto en serie de Taylor:

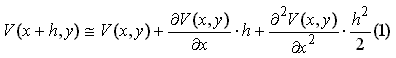
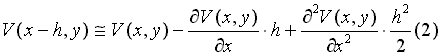
    Sumando miembro a miembro (1) y (2), agrupando y despejando el término en derivada segunda resulta:

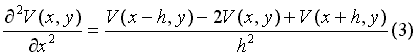
    De forma similar se obtiene la expresión para la coordenada “y”:

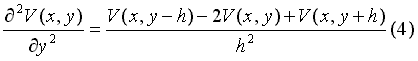
    Recordando la ecuación de Poisson:

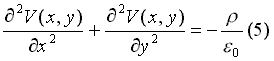
    sustituyendo las derivadas segunda por sus equivalentes (3) y (4) podemos expresarla en la siguiente forma:  

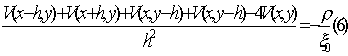
    Siendo que la carga es nula en la región considerada vale la ecuación de Laplace, verificándose que:

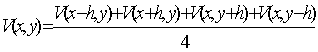     (7)

    Lo que significa que el valor del potencial en un punto es la media de los potenciales en los puntos circundantes.

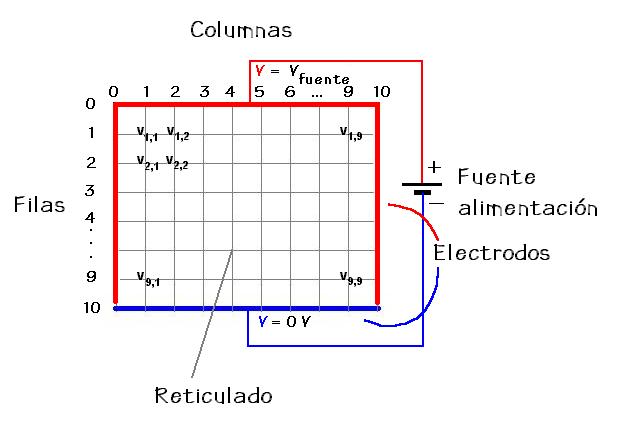
    Para aplicar éste método se debe hacer un reticulado trazando líneas paralelas a las que limitan la región de interés y espaciadas a igual distancia, h, una de otra, como lo muestra la FIG.1. Cuanto menor sea h mejor serán los resultados obtenidos.

FIG.1.- CONSTRUCCION DEL RETICULADO

    Este reticulado define una matriz de dimensiones N filas x M columnas. A cada elemento de la matriz (nodo) le corresponderá un valor experimental del potencial entre los electrodos. 

    Las condiciones de contorno para nuestro caso particular, están estipuladas por el potencial aplicado a los electrodos. Por tanto, en el cálculo teórico supondremos una superficie límite con potenciales

                                                  V_0,j = V_i,0 = V_i,10 =  V_fuente  ;  V_10,j= 0V

    Se calcularán los potenciales de puntos interiores a la superficie límite, sobre la cual los valores del potencial son conocidos. Por ejemplo, el potencial V_1,1 lo calculamos por:

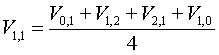        (8)

    donde, como primera aproximación tomamos V_1,2 = V_2,1 = 0  y  V_0,1 = V_1,0 = V_fuente , dado que estos puntos se encuentran sobre los electrodos.

    Así mismo, el potencial V_1,2 será el valor medio entre los siguientes potenciales vecinos:  V_0,2 = V_fuente, V_1,3= V_2,2 = 0 , y  V_1,1 = valor obtenido anteriormente de (8).

    Este procedimiento se repite para cada punto del retículo.

    Este conjunto de potenciales calculados se utiliza para realizar una nueva secuencia de cálculo obteniéndose un nuevo conjunto de valores de potencial o segunda iteración.

    Siguiendo este procedimiento iterativo por sustitución, los valores calculados de un mismo potencial, tenderán a lo largo de sucesivas iteraciones a un valor de equilibrio.

    Para nuestro caso práctico continúe el cálculo hasta que el valor del potencial en un mismo punto se estabilice luego de tres pasos consecutivos en las tres últimas cifras decimales (pues la precisión del voltímetro es de aproximadamente 0.01V). Esos valores serán finalmente, los calculados por diferencias finitas.

Material a utilizar

•  Fuente de alimentación.

• Cubeta para la práctica  de campo eléctrico.

• Electrodos especiales.

• Voltímetro.

• Cables de Conexión.

• Computadora con los utilitarios necesarios.

 Técnica Operatoria

    Mapear el campo eléctrico siguiendo el procedimiento descripto en la guía de laboratorio de “Mapéo del Campo Eléctrico” pero ahora utilizando los electródos provistos con el equipo.

    Establezca, en el espacio entre los electrodos, un reticulado apropiado (preferentemente de 9 x9) y mida el potencial en cada nodo empleando la punta exploradora. 

    Con los valores obtenidos forme la matriz de datos experimentales, determinada de la siguiente manera:

    - Si tenemos N x M puntos experimentales medidos con el voltímetro, la matriz correspondiente tendrá (N+2) filas y (M+2) columnas.  La primera y última fila y la primera y última columna corresponden a los potenciales de los electrodos (FIG.1).

    Con los demás puntos se establecerá una correspondencia biunívoca entre la posición de dichos puntos donde se midió el potencial y la posición del elemento de matriz dentro del arreglo.

Análisis de los resultados

        La matriz de datos experimentales se introducirá por teclado de la PC en un utilitario matemático EXCEL a fin de lograr:

                                i) un gráfico del potencial  V(x,y).

                                ii) un gráfico aproximado de las curvas equipotenciales experimentales.

    Empleando la planilla de cálculo EXCEL, proceda a la obtención de la matriz teórica de la siguiente manera:

            a) De formato al bloque correspondiente a  la matriz de los valores teóricos N+2 filas por M+2 columnas.

            b) Coloque el valor de los potenciales de los electrodos en las filas y columnas correspondientes (primera y última filas y primera y última columnas).

            c) Calcule el potencial en un punto interior empleando la  fórmula (8)- la planilla inicialmente tomará como potencial cero el de los puntos no calculados.-

            d) Copie la fórmula para todas las celdas del reticulado.-

            e) Cálculo iterativo: En el Menú principal de EXCEL, entre en Herramientas  y seleccione Opciones. En la ventana de dialogo desplegada elija la solapa rotulada Calcular y habilite Iteración (eligiéndolo con el botón izquierdo del ratón). Al dar Aceptar el utilitario procederá automáticamente al recálculo del reticulado completo hasta que los potenciales sobre todos los puntos se mantengan constantes. La matriz resultante corresponde a los valores teóricos calculados por diferencias finitas.

            f)  Con los datos calculados grafique el potencial V(x,y) y las equipotenciales teóricas correspondientes.

            g) Compare los gráficos y matrices teóricos y experimentales.

            h) Determine la matriz correspondiente a los errores absolutos y relativos, grafíquelas y discuta los resultados obtenidos.

            i) Discuta las posibles causas de error en la experiencia y en los cálculos.

EMPLEO DEL UTILITARIO "AMBOE"

            a) Ejecute el programa seleccionando el icono rotulado Amboé en la ventana de trabajo Física IV.

            b) Reproduzca la forma de los electrodos mediante una distribución de cargas

                discreta tal como la mostrada en la FIG.3.

            c) Seleccione la opción Líneas Equipotenciales y obtenga el gráfico (FIG.4).

            d) Imprima y compare los resultados con los obtenidos anteriormente. Explique las diferencias cualitativas entre los diferentes métodos.

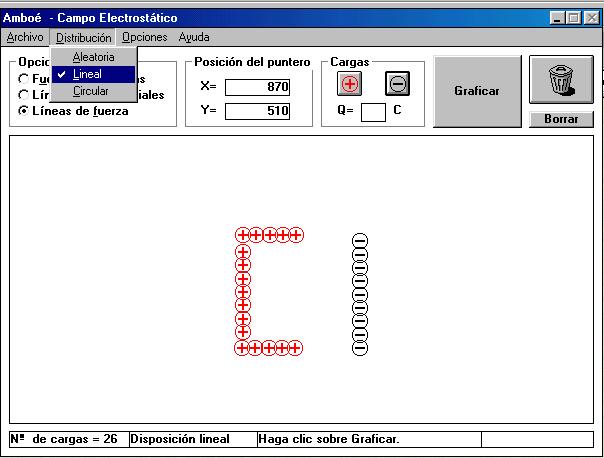
Fig.3. Simulación de los electrodos utilizados en la experiencia

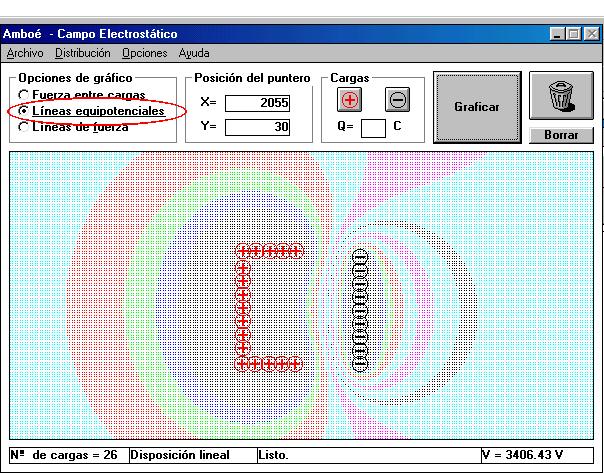
FIG.4.- Grafica de las lineas equipotenciales simuladas 

CuestionariO:

1- Deduzca la ecuación de Poisson a  partir de la ley de Gauss diferencial y dé la relación entre campo y potencial eléctrico.

2- Escriba la ecuación de Laplace. ¿En qué situación física puede aplicarse?. Dé ejemplos.

3- Qué factores influyen en la  exactitud de los potenciales calculados por diferencias finitas?

BIBLIOGRAFIA

• "Fundamentos de electricidad y magnetismo", A. Kip.

• "Electricidad y magnetismo", Sears.

• “University Physics”, Sears, Zemansky, Young.

• Física - Fundamentos y Aplicaciones, Tomo  II.  Eisber  y  Lerner (Cap. 21).

• Física, Tomo II. Feyman (Cap. 6 y 7).

• Campos y ondas. Ramo, Whinnery y Van Duzer

Abrir planilla EXCEL

ELECTRCIDAD Y MAGNETISMO

Hoja  de datos

SOLUCION DE LA ECUACION DE LAPLACE

ddp entre los electrodos : ....................... V (CON AGUA EN LA CUBETA Y FUENTE CONECTADA)

Escala del voltímetro: ..................... V

Matriz experimental

Puntos experimentales del mapéo: