Problemas resueltos de termodinámica

a. ¿Qué es el calor latente de una sustancia? ¿y el calor específico?

b. ¿Es posible transformar todo el calor en trabajo en un ciclo? Razona la respuesta.

c. ¿En qué casos se mantiene constante la temperatura de un cuerpo al que suministramos calor?

En un vaso de cobre, que pesa 1.5 kg, contiene un bloque de hielo de 10 kg a la temperatura de -10 ºC, se inyecta 5 kg de vapor de agua a 100 ºC.

• Determinar el estado de la mezcla.
• Determinar la variación de entropía

Calor específico del cobre 397 J/kg ºK. Calor de fusión del hielo 334 400 J/kg. Calor específico del agua 4180 J/kg ºK. Calor específico del hielo 2090 J/kg ºK.Calor de licuefación del vapor del agua 2 257 200 J/kg.

Un trozo de hielo de 583 cm³ a 0 ºC se calienta y se convierte en agua a 4 ºC. Calcular el incremento de energía interna y entropía que ha experimentado.

Datos: densidad del hielo 0.917 gr/cm³, del agua 1 gr/cm³, calor de fusión del hielo 80 cal/g.

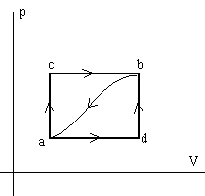Cuando un sistema pasa del estado a al b a lo largo de la transformación acb recibe una cantidad de calor de 20000 cal y realiza 7.500 cal de trabajo.

• ¿Cuánto calor recibe el sistema a lo largo de la transformación adb, si el trabajo es de 2500 cal?
• Cuando el sistema vuelve de b hacia a, a lo largo de la transformación en forma de curva, el trabajo es de 5000 cal. ¿Cuánto calor absorbe o libera el sistema?
• Si Ua=0 y Ud=10000 cal hállese el calor absorbido en los procesos ad y db.

Nota: no hace falta ningún dato de p y V para resolver el problema

Consideremos helio (gas perfecto monoatómico cv=3R/2) en el estado inicial A: PA=10⁵ Pa, VA=10^-2 m³ y TA=300 K. Se llevan a cabo las siguientes transformaciones:

• A ® B: Transformación isoterma reversible siendo VB=2 10^-2 m³

• B ® C: Transformación isócora (V=cte) reversible siendo TC=189 K

• C ® A: Transformación adiabática reversible, que devuelve al gas a sus condiciones iniciales.

a) Determinar el número de moles de helio, confeccionar una tabla en la que aparezcan los valores P, V y T en los tres estados A, B y C, y dibujar el ciclo en el diagrama P-V.

b) Calcular, en unidades del sistema internacional, de forma directa (siempre que sea posible) el trabajo W, el calor Q, y la variación de energía interna DU, del gas para cada uno de los procesos.

c) Determinar el rendimiento de este ciclo como motor térmico y comparar el resultado con el de un motor de Carnot que funcione entre las dos temperaturas extremas del ciclo.

Dato: R=8.33 J/(mol K)

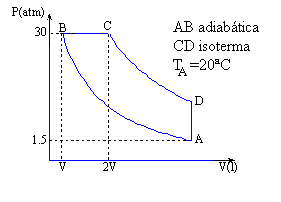Una máquina térmica trabaja con 3 moles de un gas monoatómico, describiendo el ciclo reversible ABCD de la figura. Sabiendo que VC = 2 VB: • Calcular el valor de las variables termodinámicas desconocidas en cada vértice. • Deducir las expresiones del trabajo en cada etapa del ciclo. Calcular de forma directa en cada etapa del ciclo (siempre que sea posible), el trabajo, el calor y la variación de energía interna. • El rendimiento del ciclo.

R=0.082 atm l/mol K; 1cal=4.186J; 1atm=1.013 10⁵ Pa, cv=3R/2

10 moles de un gas diatómico (C_v=5R/2) se encuentran inicialmente a una presión de P_A = 5 10⁵ Pa y ocupando un volumen de V_A = 249 10^-3 m³. Se expande adiabáticamente (proceso AB) hasta ocupar un volumen V_B = 479 10^-3 m³. A continuación el gas experimenta una transformación isoterma (proceso BC) hasta una presión P_C = 1 10⁵ Pa. Posteriormente se comprime isobáricamente (proceso CD) hasta un volumen V_D = V_A = 249 10^-3 m³. Por último, experimenta una transformación a volumen constante (proceso DA) que le devuelve al estado inicial.

1. Representar gráficamente este ciclo en un diagrama P-V.
2. Calcular el valor de las variables termodinámicas desconocidas en los vértices A, B, C y D.
3. Hallar el calor, el trabajo, la variación de energía interna, en Joules, de forma directa y/o empleando el Primer Principio, en cada etapa del ciclo.
4. Calcular el rendimiento.

R= 0.082 atm l/(mol K) = 8.314 J/(mol K) ; 1 cal = 4.186 J; 1atm = 1.013 10⁵ Pa

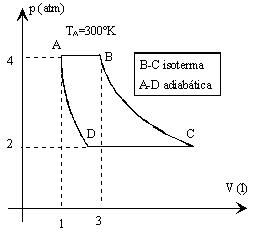En el ciclo de la figura que describe un gas ideal monoatómico Calcular el valor de las variables termodinámicas desconocidas en los vértices A, B y C. Hallar de forma directa el trabajo en cada etapa. El calor, la variación de energía interna y la variación de entropía en cada etapa del ciclo. (Expresar los resultados en Joules). Hallar el rendimiento del ciclo. R=0.082 atm l/(ºK mol) 1 cal= 4.186 J. 1 atm = 1.013 105 Pa

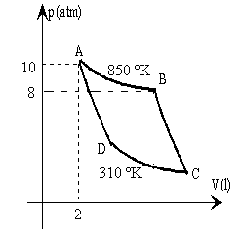Un gas diatómico, cv=5R/2, describe el ciclo de Carnot de la figura. Las transformaciones A-B y C-D son isotermas y las transformaciones B-C y D-A son adiabáticas. Hallar los valores de la presión, el volumen, y la temperatura de cada uno de los vértices A, B, C y D a partir de los datos suministrados en la figura. Calcular de forma explícita el trabajo en cada una de las transformaciones, la variación de energía interna, y el calor. Hallar el rendimiento del ciclo, y comprobar que coincide con el valor dado por la fórmula del rendimiento de un ciclo de Carnot. ¿Cuál es la razón por la que un diseñador de motores térmicos debe de conocer el ciclo de Carnot?. Dato: R=8.314 J/(ºK mol)=0.082 atm.l/(ºK mol)

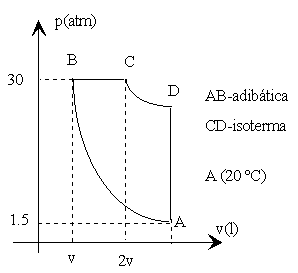Una máquina térmica trabaja sobre 3 moles de un gas monoatómico, realizando el ciclo reversible ABCD de la figura. Si el volumen del gas en el estado C es el doble del volumen del gas en el estado B. Calcular las variables desconocidas en cada vértice del ciclo. Calcular de forma directa el trabajo en cada etapa del ciclo El calor, la variación de energía interna y la variación de entropía Hállese el redimiento del ciclo.