Problemas resueltos de campo eléctrico

prev.gif (1231 bytes)home.gif (1232 bytes)next.gif (1211 bytes)

problema.gif (205 bytes)

electro_01.gif (1992 bytes) Una esfera hueca de radio interior 3 cm y radio exterior 5 cm, contiene carga uniformente distribuida por todo su volumen con una densidad de 4 10-5/p C/m3. En su centro hay una esfera conductora de 1 cm de radio cargada con -4 10-9 C.
  • Obtener, razonadamente, la expresión del campo eléctrico en las siguientes regiones r<1, 1< r<3 , 3<r<5, r>5. Indíquese la dirección y sentido del campo
  • Dibujar una gráfica de la intensidad del campo en función de la distancia radial.
  • Calcular el potencial del centro de la esfera conductora

problema.gif (205 bytes)

electro_03.gif (3018 bytes) Dos cilindros coaxiales muy largos, uno macizo y otro hueco están cargados. El primero que tiene un radio de 2 cm y es un conductor cargado con una carga por unidad de longitud de 9 10-9 C/m El hueco de radio interior 5 cm y radio exterior 8 cm, está uniformemente cargado en todo su volumen con una densidad -4/p 10-9 C/m3.
  • Determinar la expresión del campo eléctrico en las distintas regiones: r<2, 2<r<5, 5<r<8, 8<r cm.
  • Representar el campo en función de la distancia radial
  • Calcular la diferencia de potencial entre un punto situado en el eje y otro situado a 15 cm del mismo, a lo largo de la dirección radial.

problema.gif (205 bytes)Deducir de forma razonada la fórmula de la capacidad de un condensador esférico de radio R, explicando cada uno de los pasos que conducen a dicha fórmula.

Cincuenta gotas idénticas de mercurio se cargan al mismo potencial de 100 V.

problema.gif (205 bytes)

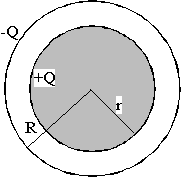electro_07.gif (2349 bytes) Un condensador esférico está formado por dos esferas concéntricas de radio interior r y radio exterior R. La primera es una esfera conductora maciza y la segunda es hueca. Determinar la fórmula su capacidad de forma razonada. Aplicar al caso en que r=5 cm, R=8 cm.

Supongamos ahora que este condensador cargado con 6 mC se une a otro inicialmente descargado de radios 4 cm y 10 cm. Determinar la carga de cada condensador después de la unión, el potencial común y la variación de energía en el proceso.

problema.gif (205 bytes)

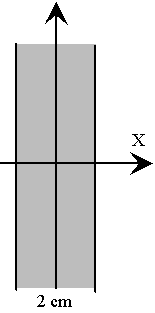electro_09.gif (2415 bytes) Una placa plana, indefinida de 2 cm de espesor, está uniformemente cargada, con una densidad de carga de 2 10-8 C/m3.
  • Obtener razonadamente, la expresión del campo eléctrico en el interior y en el exterior de dicha placa.
  • Representar el módulo del campo eléctrico en función de la distancia a la placa.
  • Hallar la diferencia de potencial entre el origen (plano de simetría de la placa) y un punto situado a 8 cm de dicho plano.

problema.gif (205 bytes)

electro_10.gif (1901 bytes) Dos cilindros coaxiales muy largos, uno macizo y otro hueco están cargados. El primero tiene un radio de 2 cm y está uniformente cargado en todo su volumen con una densidad de 4/p 10-6 C/m3. El hueco de radio interior 5 cm y de radio exterior 8 cm, es un conductor cargado con una carga por unidad de longitud de -9 10-9 C/m.
  • Determinar, de forma razonada, la expresión del campo eléctrico en las siguientes regiones: r<2, 2<r<5, 5<r<8, r>8 cm.
  • Representar el campo en función de la distancia radial.
  • Calcular la diferencia de potencial entre un punto situado en el eje de los cilindros y otro situado a 15 cm del mismo, a lo largo de la dirección radial.

problema.gif (205 bytes)

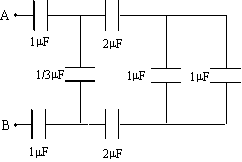electro_12.gif (2108 bytes) Calcular la capacidad equivalente del sistema de la figura. Calcular la carga y la diferencia de potencial entre las placas de cada condensador. La energía electrostática del sistema. Dato la diferencia de potencial entre el extremo A y el extremo B es de 3000 V.

problema.gif (205 bytes)

electro_02.gif (2006 bytes) Deducir de forma razonada la fórmula de la capacidad de un condensador cilíndrico fromado por dos armaduras consistentes en láminas conductoras coaxiales de longitud L, y radios a (exterior) y b (interior

Calcular la capacidad de un condensador cilíndrico de radio interior b= 3 cm, exterior a=5 cm. y longitud L=30 cm.

Supongamos ahora, dos condensadores idénticos que se conectan en paralelo, cargándose a una diferencia de potencial de 100 V, después de lo cual se aíslan de la batería. A continuación, se introduce en uno de los condensadores un dieléctrico (k=3) que llena completamente el espacio entre las placas. Calcular:

  • La carga de cada condensador antes y después de introducir el dieléctrico.
  • La diferencia de potencial después de introducir el dieléctrico
  • La energía de cada condensador antes y después de introducir el dieléctrico.

problema.gif (205 bytes)Conectamos un condensador de capacidad C, una resistencia R, y una batería de f.e. m. Vo en serie.

Sea un condensador de 1.6 mF, una resistencia de 58 KW y una batería de 14V. Se empieza a contar el tiempo cuando se cierra el interruptor