Problemas resueltos de campos dependientes del tiempo

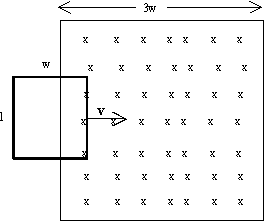 |
Una espira rectangular de dimensiones l y w y resistencia R se mueve con
velocidad constante v hacia la derecha como se muestra en la figura, penetra en una
región donde hay un campo magnético uniforme perpendicular al plano del papel y hacia
dentro de módulo B. Calcular y hacer un gráfico de:
- El flujo, la f.e.m. y la fuerza sobre la espira, en función de la posición de la
espira, es decir, cuando la espira se está introduciendo, está introducida, y está
saliendo de la región que contiene el campo magnético.
- Explíquese el mecanismo (fuerza sobre los portadores de carga) de establecimiento de la
corriente inducida en los tres casos citados.
|

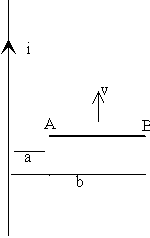 |
Sabiendo que el módulo del campo magnético producido por una corriente
rectilínea indefinida de intensidad i a una distancia r vale 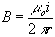
- Calcular la diferencia de potencial entre los extremos A y B de una varilla que se mueve
paralelamente a la corriente rectilínea con velocidad v.
- ¿Cuál es el potencial más alto de los dos?. Razonar las respuesta
|

 |
Se coloca un circuito de N vueltas, cada una de área S, en un campo
magnético uniforme, paralelo al eje Z, que varía con el tiempo de la forma Bz=Bo cos(wt).
- Cacular la f.e.m. inducida.
- Representar el campo magnético y la fem en función del tiempo.
- Representar en el circuito el sentido del campo y de la corriente inducida en cada
cuarto de periodo, explicando el resultado
|

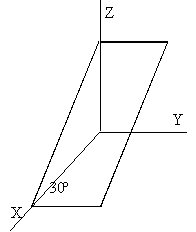
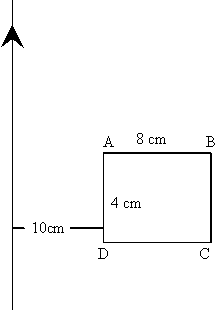
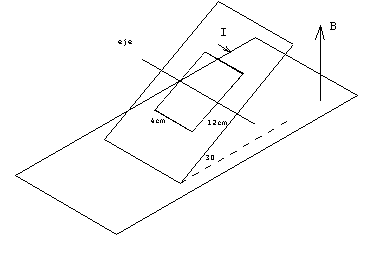
Una bobina hecha de 120 espiras rectangulares apretadas, de dimensiones 4 cm y 12 cm,
están situada en un plano que forma 30º con el plano XY. La bobina está en una región
en la que existe un campo magnético paralelo al eje Z.
·
Si el campo magnético vale 0.02 T
y por la bobina circula una corriente de intensidad 2 A. Calcular módulo, dirección y
sentido del momento de las fuerzas sobre la bobina.
·
Consideremos ahora el caso en el
que el campo es variable con el tiempo, y la bobina está fija en el plano inclinado,
según se muestra en la figura. Trazar un gráfico de la intensidad de la corriente
inducida en función del tiempo. (Tomar como positiva la intensidad de la corriente en el
sentido contrario al de las agujas del reloj). Razónese las respuestas.
Dato: la bobina presenta una resistencia de 50 W.

 |
Determinar, aplicando la ley de Ampère, el campo magnético producido por
una corriente rectilínea e indefinida de intensidad i. Una corriente rectilínea
conduce una corriente de 10 A. La espira rectangular una corriente de 2 A en el sentido de
las agujas del reloj. Calcular.
- La fuerza (módulo, dirección y sentido) que ejerce la corriente rectilínea sobre cada
uno de los lados de la espira
- El coeficiente de inducción mutua.
- Supongamos ahora, que la corriente rectilínea tiene una amplitud de 10 A y una
frecuencia de 60Hz, determinar la intensidad de la corriente inducida en la espira, si su
resistencia es de 40W.
Dibújese sobre la espira el sentido de dicha corriente cada cuarto de periodo. Dibujar en
un mismo gráfico, intensidad - tiempo, la intensidad en la corriente rectilínea y la
intensidad en la espira. Razónese las respuestas.
|

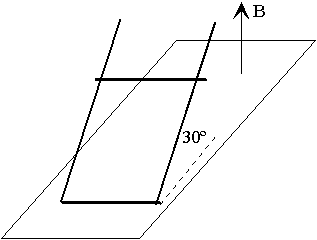 |
Una varilla conductora de masa 10 g desliza sobre carriles paralelos
distantes 20 cm y que forman un ángulo de 30º con el plano horizontal. Los carriles se
cierran por la parte inferior, tal como se indica en la figura. En la región existe un
campo magnético uniforme y perpendicular al plano horizontal de intensidad 1 T.
- Calcular la fem en función de la velocidad constante de la varilla. La intensidad de la
corriente inducida si la resistencia del circuito es de 10 W.
La(s) fuerza(s) sobre la varilla.
- ¿Cuánto valdrá la velocidad de la varilla cuando desliza con movimiento uniforme? (se
desprecia el rozamiento).
- Razonar las respuestas dibujando los esquemas
|

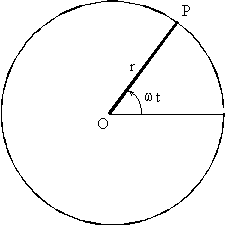 |
Una varilla de longitud r gira con velocidad angular w apoyado su extremo P en un raíl semicircular del mismo
radio. El dispositivo está situado en un campo magnético B uniforme, perpendicular al
plano del papel y dirigido hacia adentro.
- Determinar razonadamente, la fem y el sentido de la corriente inducida
- Si en un instante dado la resistencia del circuito es R. Hallar la fuerza que ejerce el
campo magnético sobre una porción infinitesimal de la varilla OP, y el momento de las
fuerzas sobre la varilla respecto del centro O. Hállese la potencia necesaria que
tendremos que suministrar para mantener la varilla girando con velocidad constante.
|

 |
Una varilla de longitud r gira con velocidad angular constante w apoyando su extremo P en un rail semicircular del mismo radio. El
dispositivo está situado en un campo magnético B uniforme, perpendicular al plano del
papel y dirigido hacia adentro. Determinar
- Mediante la ley de Faraday-Lenz, la fem y el sentido de la corriente inducida.
- Mediante el mecanismo de la corriente inducida determinar la diferencia de potencial
entre O y P. ¿Cómo se mueven los portadores de carga positivos: en la varilla y en el
conductor circular?.
- Comprobar que las respuestas (a) y (b) son concordantes.
- Determinar la intensidad de la corriente en un instante t, sabiendo que la varilla y el
rail son conductores de la misma sección y resistividad.
|

 |
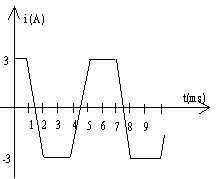 |
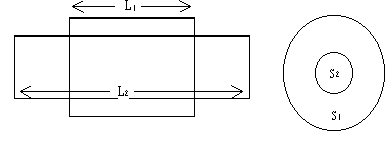
- Determinar, razonadamente la intensidad del campo magnético en el interior de un
solenoide de longitud L, y de N vueltas, por el que circula una corriente de intensidad I.
- Obtener el coeficiente de inducción mutua de dos solenoides rectos largos y
concéntricos de N1 y N2 espiras, longitud L1 y L2,
y secciones S1 y S2 respectivamente.
- Datos: n1= 100 espiras por cm, n2=150 espiras por cm. S1=
9/p cm2, S2=3/p
cm2. L1= 20 cm, L2=30 cm.
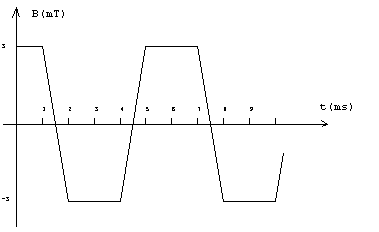
- Si por el primario, solenoide exterior, circula una corriente, como indica la figura,
obtener y hacer un gráfico de la corriente del secundario, sabiendo que su resistencia es
de 50 W. Razónese la respuesta a partir de esquemas en los que
se especifique el sentido de la corriente en el primario y en el secundario
 Explicar el funcionamiento de un transformador.
Explicar el funcionamiento de un transformador.
Una casa de campo precisa de 18 kW y toma la corriente de una red de 15 kV. Los
aparatos instalados en la casa funcionan a 220 V. El transformador que nos reduce la
tensión tiene un rendimiento del 90% y su secundario tiene 40 espiras. Calcular:
- La intensidad en el primario y en el secunadrio.
- El número de espiras del primario.

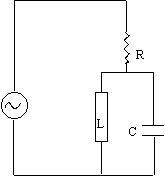 |
Usando los diagramas de vectores rotatorios, estudiar el circuito de
corriente alterna de la figura.
- Hallar la amplitud de la intensidad, y el ángulo de desfase.
- Hallar también la potencia media suministrada por la f.em.
Datos: Vo = 100 V, R= 1 W, L=0.003 H, C=0.002 F, w=120p rad/s |

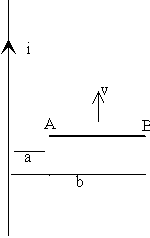







![]() Explicar el funcionamiento de un transformador.
Explicar el funcionamiento de un transformador. 